میدانیم که تمام قوانین حرکت ، چه قوانین نیوتن و چه قوانین ماکسول برای میدانهای الکترومغناطیسی متحرک ، باید با یک چارچوب مرجع همراه باشند. در عین حال ، یک فرآیند فیزیکی نباید به چارچوبی که ناظر برای مشاهده آن انتخاب کرده است، وابسته باشد. پس قوانین فیزیکی را باید به صورتی نوشت که در سیستمهای مختصات مختلف شکلشان حفظ شود. بنابراین تبدیلی که با اعمال آن فرم ریاضی قانون فیزیکی در چارچوبهای مختلف لخت ، ثابت بماند، اهمیت اساسی دارد. تبدیل که در زمان نیوتن رواج داشت، تبدیلات گالیله بود:
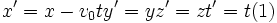
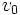 در جهت x حرکت میکنند، بیان شده است.
در جهت x حرکت میکنند، بیان شده است. اینکه قوانین نیوتن تحت تبدیلات گالیله ناوردا هستند، مطلبی شناخته شده بود. با وجود این نیوتن معتقد بود که قوانینش به یک چارچوب مرجع مطلق وابسته است. البته این فکر کاملا متافیزیکی است، چون خود او اصل نسبیت در مکانیک را وضع کرده بود که بر طبق آن ، تعیین حرکت مستقیم الخط یک جسم متحرک ، یا یک چارچوب مرجع ، نسبت به این سیستم مطلق غیر مطلق ناممکن است.
برای مثال شتاب و نیرو در این دو چارچوب مرجع مشابهاند، چون طبق روابط (1) داریم: 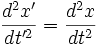
پس F"=ma تحت تبدیلات گالیله به صورت F=ma در میآید، یعنی تحت این تبدیلات ناوردا است. دلیل این ناوردایی عدم ظهور سرعت در معادله حرکت است.
اگر تبدیلات گالیله را در مورد معادلات ماکسول اعمال کنیم، شکل معادلات در سیستمهای مختصات مختلف فرق خواهد کرد، چون سرعت انتشار امواج الکترومغناطیسی در معادلات ظاهر میشود، لذا وقتی این سرعت به صورت برداری جمع شود، در سیستمهای مختصات مختلفی که نسبت به هم حرکت میکنند، مقادیر مختلفی خواهد داشت. تفاوت سرعت چند مفهوم ضمنی دارد، اول اینکه تشخیص چارچوب مرجع مطلق به روش الکترومغناطیسی یا نوری ممکن خواهد بود. در آن زمان فرض میشد که نور برای انتشار نیاز به محیط خاصی دارد، و این محیط اتر نامیده میشد.
این حقیقت که معادلات ماکسول تحت تبدیلات گالیله تغییر میکنند، مستلزم این بود که سیستم مرجعی وجود داشته و اتر نسبت به آن ساکن باشد. سرعت نور در این چارچوب مطلقا ساکن ، C است و احتمالا در یک چارچوب مرجع دیگر C نخواهد بود. اینکه سرعت نور در دو سیستم مختصات مختلف تحت تبدیلات گالیله متفاوت است، از رابطه (1) پیداست. اگر سرعت نور در یک چهارچوب S (بدون پریم) dx/dt باشد، در چهارچوب "S که نسبت به S با سرعت 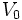 حرکت میکند، به صورت
حرکت میکند، به صورت 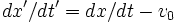 خواهد بود.
خواهد بود.
با این حال آزمایش فیزو ، آزمایش مایکلسون - مورلی و آزمایشهای متعدد دیگری که هدفشان بررسی دقت معادلات ماکسول در چارچوبهای مرجع متحرک بود، نشان داد که بیشک سرعت نور در تمام جهتها و در تمام سیستمهای مرجع متحرک یکسان است. بنابر این نتیجه میگیریم که معادلات ماکسول باید در تمام مختصات لخت شکل خود را حفظ کند.
لورنتس که سعی میکرد تبدیلات گالیله را بهبود بخشد، تبدیل جدیدی یافت که تحت آن معادلات ماکسول در سیستمهای مختصات مختلفی که نسبت به هم حرکت دارند، تغییر نمیکرد و به این ترتیب اساس نسبیت خاص بنا نهاده شد. این تبدیل اکنون تبدیلات لورنتس نامیده میشود: 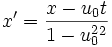
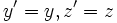
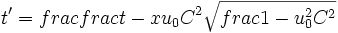
کمی بعد پوانکاره نشان داد که تمام معادلات الکترودینامیک تحت تبدیلات لورنتس شکل خود را حفظ میکند. یک امتحان ساده نشان میدهد که در تبدیلات لورنتس 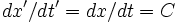 . انیشتین در سال 1905 این فکرها را تعمیم داد و به صورت نسبیت خاص فعلی در آورد. او نشان داد که با پذیرفتن نسبیت نیوتن ، میتوان تبدیلات لورنتس را بدست آورد. انیشتین فرض کرد که سرعت نور یک ثابت جهانی و مستقل از حرکت چشمه آن است.
. انیشتین در سال 1905 این فکرها را تعمیم داد و به صورت نسبیت خاص فعلی در آورد. او نشان داد که با پذیرفتن نسبیت نیوتن ، میتوان تبدیلات لورنتس را بدست آورد. انیشتین فرض کرد که سرعت نور یک ثابت جهانی و مستقل از حرکت چشمه آن است.
گرچه ریشه نسبیت خاص در الکترومغناطیس بود، ولی روش انیشتین وابستگی صریحی به الکترودینامیک نداشت. چون معادلات ماکسول تنها یکی از قوانین فیزیکی است که اصول نسبیت خاص آن را در بر میگیردف بنابر این نسبیت خاص نتایج وسیعی داشت. به این ترتیب مفهوم اتر از بین رفت.
بر اساس اصل دوم نسبیت خاص مفهوم کلاسیکی زمان ، به عنوان یک متغیر مستقل از دستگاه مختصات و حرکت نسبی از بین رفت و مفهوم پیچیده و مشکل فضا_زمان جانشین آن شد. در همزمانی وقایع باید تجدید نظر کرد. وقایعی که در یک سیستم مختصات همزمان هستند، لزوما در سیستم دیگری که نسبت به اولی حرکت دارد، همزمان نیستند. این ایدهها چنان تکان دهنده بود که خیلیها به تندی با آن مخالفت کردند و شاید هنوز هم میکنند. برای ارائه فرضیهای که به اصل موضوع دوم محتاج نباشد، کوششهای هوشمندانه بسیاری شد. تاکنون آزمایشهای مختلف و متعددی پیشبینیهای نسبیت خاص را تصدیق کردهاند، طوری که تنها میتوان فرضیههای سازگار با نسبیت خاص را در نظر گرفت.
قوانین کلاسیک الکترودینامیک که تحت تبدیلات گالیله ناوردا هستند، با تبدیلات لورنتس نیز ناوردا میمانند. ولی معادلات مکانیک کلاسیک که تحت تبدیلات گالیله ناوردا بودند، اکنون با تبدیلات لورنتس ناوردا نیستند، یعنی یا باید آنها را دور ریخت و یا با معادلات نسبیتی جایگزین کرد. در معادلات نسبیتی جرم یک جسم m که با سرعت v حرکت میکند، با جرم آن در حالت سکون ، 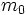 ، به صورت زیر مرتبط است:
، به صورت زیر مرتبط است:
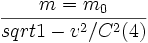
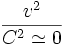 معادلات نسبیتی به قوانین حرکت نیوتن تبدیل میشوند. لزوم تصحیح نسبیتی در قوانین حرکت خیلی زود با آزمایش تائید شد. برای مثال الکترونها را میتوان در یک شتابدهنده شتاب داد و سرعتشان را نزدیک به سرعت نور رساند، طوری که جرمشان چند هزار برابر شود.
معادلات نسبیتی به قوانین حرکت نیوتن تبدیل میشوند. لزوم تصحیح نسبیتی در قوانین حرکت خیلی زود با آزمایش تائید شد. برای مثال الکترونها را میتوان در یک شتابدهنده شتاب داد و سرعتشان را نزدیک به سرعت نور رساند، طوری که جرمشان چند هزار برابر شود. با بسط رابطه (4) یک جمله 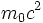 نتیجه میشود که انیشتین ، لویس و دیگران آن را انرژی سکون
نتیجه میشود که انیشتین ، لویس و دیگران آن را انرژی سکون 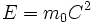 تشخیص دادند. پیشبینی این انرژی بسیار زیاد جرم ، در آزمایشهای شکافت (فیزیون) و ابزارهای هستهای تایید شد.
تشخیص دادند. پیشبینی این انرژی بسیار زیاد جرم ، در آزمایشهای شکافت (فیزیون) و ابزارهای هستهای تایید شد.
شاید بهترین و سادهترین مثال نشان دهنده 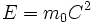 هنگامی باشد که یک الکترون و پاد الکترون (پوزیترون) ، که جرم هر دو
هنگامی باشد که یک الکترون و پاد الکترون (پوزیترون) ، که جرم هر دو 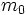 است، ترکیب میشوند. این دو همدیگر را نابود میکنند و دو اشعه گاما بوجود میآید. انرژی اشعه گاما با انرژی سکون دو ذره قبل از برخورد ،
است، ترکیب میشوند. این دو همدیگر را نابود میکنند و دو اشعه گاما بوجود میآید. انرژی اشعه گاما با انرژی سکون دو ذره قبل از برخورد ، 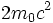 ، برابر است.
، برابر است.
تبدیلات گالیله
در برسی حرکت هر ذره باید یک چارچوب مرجع تعین کنیم که این چارچوب به عنوان ناظر در فیزیک تعبیر میشود. بعد از تعیین چارچوب مرجع به راحتی میتوانیم حرکت را مورد برسی قرار دهیم. البته لازم به ذکر است که در مورد هر حرکت ، چارچوب خاصی متناسب با نوع حرکت باید بکار ببریم. این مسئله نه تنها در مورد حرکت بلکه در مورد تمام رویدادها و پدیدههای فیزیکی مطرح است.
به عنوان مثال برای اینکه بتوانیم در الکترو مغناطیس مقدار نیروی وارد بر یک جسم باردار را محاسبه کنیم، ابتدا باید یک چارچوب متناسب با سیستم تعریف کرده ، سپس پدیده را مورد برسی قرار دهیم. حال سوال این است که اگر این چارچوب مرجع تغییر بکند (به عنوان مثال اگر چارچوب مرجع منتقل شود) ، در این صورت چه تغییری در برسی حاصل خواهد شد. این مسئله بوسیله قواعد تبدیل بیان میشود.
معادلاتی که در فیزیک کلاسیک مختصات فضا و زمان دو دستگاه مختصات را ، که با سرعت ثابت نسبت به یکدیگر حرکت میکنند به هم مربوط میسازند، تبدیلات گالیله یا نیوتنی نامیده میشوند. هر ناظر با مشخص کردن مکان و زمان یک پدیده فیزیکی ، مانند یک بمب کوچک ، هر رویدادی را میتواند توصیف کند. اگر مختصات فضایی و زمانی یک رویداد ، از نظر ناظر S1 بصورت:
|
لازم به ذکر است که تبدیلات سرعت و شتاب نیز با مشتق گیری از روابط فوق حاصل میشود.
هموردایی مکانیک کلاسیک در تبدیلات گالیله
در فیزیک به عنوان یک اصل پذیرفته میشود که ، قوانین فیزیک در تمام دستگاههای لخت یکسان ، یا هموردا ، هستند. یعنی شکل ریاضی یک قانون فیزیکی یکسان باقی میماند. به عبارت دیگر میتوان گفت که باید قوانین فیزیک تحت تبدیلات گالیله یکسان باقی بمانند. از جمله قوانین فیزیکی که تحت این تبدیلات فرم ریاضی خود را حذف میکنند، قوانین بقای اندازه حرکت خطی و قانون بقای انرژی است. همچنین قانون دوم نیوتن نیز که قانون بقای اندازه حرکت خطی از آن نتیجه میشود، فرم ریاضی خود را حفظ میکند.
به عبارت دیگر میتوان گفت که تبدیلات گالیله و مکانیک کلاسیک مستلزم آن هستند که سه کمیت اساسی در آزمایشهای فیزیکی ، یعنی طول ، زمان و جرم همگی از حرکت نسبی هر ناظری مستقل باشد. البته فیزیک نسبیت انیشتن در این عقیده تجدید نظر میکند. و بجای طول ، زمان ، جرم و انرژی، دو قانون بقای جدید بوجود میآورد. یعنی طول و زمان را باهم ادغام کرده و یک کمیت ناوردا در فضای چهار بعدی بوجود میآورد و نیز قانون بقای جرم و انرژی را هم یکجا در رابطه هم ارزی جرم و انرژی بیان میکند.
در اوایل توسعه نظریه موجی نور این سوال مطرح شد که آیا امواج الکترومغناطیسی در محیط واقعی منتشر میشوند یا در اتر. اگر انتشار در اتر انجام میشد، در آن صورت فرض بر این بود که محورهای مختصات واقع در آن محیط باید چارچوب مشخصی را تشکیل دهند، بطوری که همه ناظرها نسبت به آن ساکن یا در حرکت نسبی باشند. حال به خوبی میدانیم که همه کوششهای تجربی برای کشف وجود یک محیط ساکن که در آن امواج الکترومغناطیسی منتشر شوند با شکست مواجه شد.
لذا نتیجه میگیریم که از نظر هر ناظر لخت ، نور در فضا با تندی استاندارد c ، بدون توجه به حالت یکنواخت او نسبت به هر چارچوب مختصات دیگر بطور همسانگرد منتشر میشود. ناوردایی سرعت نور بر این شرط فیزیکی دلالت دارد که معادلههای الکترومغناطیس باید در اثر تبدیل مختصات هر چارچوب مرجع ، در حرکت یکنواخت نسبت به چارچوب اصلی به طریقی تبدیل شوند، که صورت اصلیشان حفظ شود. اما معادله موج که از معادلات ماکسول حاصل میشود ، تحت تبدیلات گالیله شکل ریاضی خود را حفظ نمیکند. بنابراین ، بجای استفاده از تبدیلات گالیله از تبدیلات لورنتس که یک جایگزین قوی برای تبدیلات گالیله است، استفاده میکنیم.
بر اساس دلایل فوق میتوان چنین نتیجه گرفت که ، تبدیلات گالیله نمیتوانند یک تبدیل جامع و کامل باشد. لذا باید از یک تبدیل جامعتر که قادر به توضیح تمام قوانین فیزیک باشد، استفاده کنیم. چنین تبدیلی ، تبدیلات لورنتس میباشد. این تبدیل بر اساس دو اصل ، ناوردایی سرعت نور و اصل هم ارزی ایجاد شده است.
تبدیلات لورنتس (Lorentz transformations)
در اواخر قرن نوزدهم ، بعد از اینکه نظریه الکترومغناطیس کلاسیک به صورت کنونی اش توسعه یافت، نیاز به یک نظریه نسبیت رضایتبخش در فیزیک احساس شد. در آن زمان آشکار شد که مشاهدات تجربی انتشار نور در ارتباط با اثرهای حرکت ناظر نسبت به محیطی که فرض میشد نور در آن حرکت میکند تناقضهایی با عقاید رایج آن زمان دارد. برای داشتن توصیفی از حرکت نور که با تجربه سازگار باشد، لازم شد قانون تبدیل پیشنهادی لورنتس که مختصات چارچوبهای دارای حرکت نسبی یکنواخت را به هم مربوط میسازد، پذیرفته شود. این قانون تبدیل ، به نام تبدیلات لورنتس معروف است.
به طور خلاصه میتوان گفت که ، تبدیل مختصات در چارچوبهای لخت که از نظر نسبیت صحیح باشد، توسط دو اصل حاکم زیر تعیین میشود:
با اعمال دو اصل فوق میتوان تبدیلات لورنتس را به روش مقدماتی بدست آورد. بنابراین اگر دو چارچوب مختصه متعامده E1 و E2 ، را که با سرعت نسبی ثابت U در امتداد محور ایکس (X) شان حرکت میکنند در نظر بگیریم. در اینصورت هرگاه مختصات یک رویداد در چارچوب اول را با X1y1 z1 t1 و مختصات همان رویداد در چارچوب دوم را با x2 y2 z2 t2 نشان دهیم، در اینصورت تبدیل لورنتس که بیانگر روابط تبدیل بین مختصات رویداد مورد نظر هنگام رفتن از یک چارچوب به چارچوب دیگر است، به صورت زیر خواهد بود.
Z2=z1
T2=(t1+Vx/c2)/1-(v/c)21/2
از فیزیک نوین میدانیم که در سرعتهای نزدیک به سرعت نور ، کمیتهای طول ، زمان ، جرم دیگر مفهوم کلاسیکی مطلق بودن خود را به طور کامل از دست داده و تابع سرعت میباشند. به گونهای که انقباض طول ، اتساع زمان و افزایش جرم ملاحظه میگردد. اما در عوض کمیتی به نام عنصر جهان خط وجود دارد که مستقل از سرعت بوده و یک کمیت ناوردا میباشد. شرط ناوردایی این کمیت تحت تبدیلات لورنتس ایجاب می کند که اگر مختصات فضا زمان یک رویداد را بصورت (t, x, y, z ) نشان دهیم، این کمیت ناوردا بصورت زیر باشد.
کمیت فوق در چارچوبهای لخت ناوردا است. معلوم میشود که هرگاه کمیت فوق با نقاط واقع در مسیر باریکه نور در حال انتشار متناظر باشد، ناظرهای واقع در تمام چارچوبهای لخت مقدار ثابت مشابهی را برای آن ثبت میکنند.
همچنین ملاحظه کردیم که به منظور استفاده از مزایای دستگاه متعامد و خواص تبدیل آنها در مختصات چهار بعدی رویدادها در فضا - زمان مینکوسکی ترفند استفاده از مختصه زمانی موهومی را پیشنهاد کرد. به عبارت دیگر مختصات فضا - زمان یک رویداد را باید به صورت (ict,x,y,z) نمایش دهیم.
کلمات کلیدی: کوانتوم، فیزیک نوین